深度学习入门+前四章

本文最后更新于：2023年8月20日 中午

第一章 Python 入门

1.1 Python 解释器

Python 解释器也被称为“对话模式”，用户能够以和 Python 对话的方式进行编程。

1.1.1 数据类型

type() 查看数据类型

image.png

1.1.2 变量

Python 是属于“动态类型语言”的编程语言，所谓动态，是指变量的类型是根据情况自动决定的。另外，“#”是注释的意思，它后面的文字会被 Python 忽略。

1.1.3 列表

就是数组

image1.png

此外，Python 的列表提供了切片（slicing）这一便捷的标记法。使用切片不仅可以访问某个值，还可以访问列表的子列表（部分列表）。
#python语法/列表

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> print(a)
[1, 2, 3, 4, 99]
>>> a[0:2] # 获取索引为 0 到 2（不包括 2 ！）的元素
[1, 2]
>>> a[1:] # 获取从索引为 1 的元素到最后一个元素
[2, 3, 4, 99]
>>> a[:3] # 获取从第一个元素到索引为 3（不包括 3 ！）的元素
[1, 2, 3]
>>> a[:-1] # 获取从第一个元素到最后一个元素的前一个元素之间的元素
# a[:-1] 就相当于 a[0:4],-1应该指的是倒数第1个元素
[1, 2, 3, 4]
>>> a[:-2] # 获取从第一个元素到最后一个元素的前二个元素之间的元素
[1, 2, 3]

1.1.4 字典

键值对 {‘idex’:value}

1
2
3
4
5
6
>>> me = {'height':180} # 生成字典
>>> me['height'] # 访问元素
180
>>> me['weight'] = 70 # 添加新元素
>>> print(me)
{'height': 180, 'weight': 70}

1.1.5 布尔型

值: True or False

运算符: and, or 和 not(针对数值的运算符有 +、-、*、/ 等)

1
2
3
4
5
6
7
8
9
10
>>> hungry = True # 饿了？
>>> sleepy = False # 困了？
>>> type(hungry)
<class 'bool'>
>>> not hungry
False
>>> hungry and sleepy # 饿并且困
False
>>> hungry or sleepy # 饿或者困
True

1.1.6 if 语句

注意: 用 4 个空白字符的缩进(tab) 来代替大括号

1
2
3
4
5
6
7
8
9
10
11
12
13
14
>>> hungry = True
>>> if hungry:
...print("I'm hungry")
...
I'm hungry
>>> hungry = False
>>> if hungry:
...print("I'm hungry") # 使用空白字符进行缩进
... else:
...print("I'm not hungry")
...print("I'm sleepy")
...
I'm not hungry
I'm sleepy

1.1.7 for 语句

用 “ for··· in ··· ：” 的结构,同样用缩进代替大括号

1
2
3
4
5
6
>>> for i in [1, 2, 3]:
...print(i)
...
1
2
3

1.1.8 函数

可以将一连串的处理定义成函数（function）。

1
2
3
4
5
>>> def hello(object):
... print("Hello " + object + "!")
...
>>> hello("cat")
Hello cat!

关闭 Python 解释器,Linux: ctrl_D ; Windows: ctrl_Z, 再按 Enter

1.2 Python 脚本文件

Python 解释器干点简单的还行,想进行一连串的处理时,因为每次都需要输入程序，所以不太方便. 这时，可以将 Python 程序保存为文件，然后（集中地）运行这个文件。

1.2.1 保存为文件

在命令行中

1
2
3
$ cd ~/deep-learning-from-scratch/ch01 # 移动目录
$ python hungry.py
I'm hungry!

1.2.2 类

python 中使用 class 关键字来定义类，类要遵循下述格式（模板）。
#python语法/类

1
2
3
4
5
6
7
class 类名：
  def __init__(self, 参数 , …): # 构造函数
 ...
  def 方法名 1(self, 参数 , …): # 方法 1
 ...
  def 方法名 2(self, 参数 , …): # 方法 2
 ...

在方法的第一个参数中明确地写入表示自身（自身的实例）的 self 是 Python 的一个特点.

self 相当于一个实例的 this 指针

1.3 Numpy

在深度学习的实现中，经常出现数组和矩阵的计算。NumPy 的数组类（numpy.array）中提供了很多便捷的方法，在实现深度学习时，我们将使用这些方法。本节我们来简单介绍一下后面会用到的 NumPy

1.3.1 导入 Numpy

NumPy 是外部库。这里所说的“外部”是指不包含在标准版 Python 中。

1
>>> import numpy as np  # as相当于命个别名

1.3.2 生成 Numpy 数组

用 np.array() 生成, 接收列表为参数

1
2
3
4
5
>>> x = np.array([1.0, 2.0, 3.0])
>>> print(x)
[ 1. 2. 3.]
>>> type(x)
<class 'numpy.ndarray'>

1.3.3 NumPy 的算术运算

1
2
3
4
5
6
7
8
9
10
>>> x = np.array([1.0, 2.0, 3.0])
>>> y = np.array([2.0, 4.0, 6.0])
>>> x + y # 对应元素的加法
array([ 3., 6., 9.])
>>> x - y
array([ -1., -2., -3.])
>>> x * y # element-wise product 对应元素的乘法
array([ 2., 8., 18.])
>>> x / y
array([ 0.5, 0.5, 0.5])

当 x 和 y 的元素个数相同时，可以对各个元素进行算术运算。如果元素个数不同，程序就会报错，所以元素个数保持一致非常重要。

除了 elment-wise 运算,也可以和单一的数值 (标量) 组合起来进行运算

1
2
3
4
>>> x = np.array([1.0, 2.0, 3.0])
>>> x / 2.0
array([ 0.5, 1. , 1.5])
# 就是一个向量除以一个标量

这个功能也被称为广播（详见后文）。

1.3.4 NumPy 的 N 维数组

NumPy 也可以生成多维数组。比如，可以生成如下的二维数组（矩阵）。

1
2
3
4
5
6
7
8
>>> A = np.array([[1, 2], [3, 4]])
>>> print(A)
[[1 2]
 [3 4]]
>>> A.shape
(2, 2)
>>> A.dtype
dtype('int64')

矩阵 A 的形状可以通过 shape 查看，矩阵元素的数据类型可以通过 dtype 查看.

矩阵的算数运算和上面一维数组相同

本书基本上将二维数组称为“矩阵”，将三维数组及三维以上的数组称为“张量”或“多维数组”。

1.3.5 广播

一个矩阵乘以一个标量,这个标量会得到扩展

![image.png](深度学习入门 + 前四章 +678689c2-468f-49f5-ba9d-fc832005bf72/image 2.png)

一个矩阵乘以一个向量,这个向量会得到扩展

![image.png](深度学习入门 + 前四章 +678689c2-468f-49f5-ba9d-fc832005bf72/image 3.png)

1.3.6 访问元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
   >>> X = np.array([[51, 55], [14, 19], [0, 4]])
   >>> print(X)
   [[51 55]
   [14 19]
   [ 0 4]]
   >>> X[0] # 第 0 行
   array([51, 55])
   >>> X[0][1] # (0,1) 的元素
   55

​   ```
​    

   使用for语句. 按行显示
    

   ```Python
   >>> for row in X:
   ...print(row)
   ...
   [51 55]
   [14 19]
   [0 4]

使用数组. 用flatten将矩阵转换为一维数组. 索引用数组的形式更为简洁.

运用这个标记法,可以获取满足一定条件的元素. 对 Numpy 数组使用不等号运算符,结果会得到一个布尔型的数组.

1
2
3
4
5
6
7
8
9
10
11
12
>>> X = np.array([[51, 55], [14, 19], [0, 4]])
>>> X = X.flatten() # 将 X 转换为一维数组
>>> print(X)
[51 55 14 19 0 4]
>>> X[np.array([0, 2, 4])] # 获取索引为 0、2、4 的元素
array([51, 14, 0])

# 从X中抽出大于15的元素
>>> X > 15 
array([ True, True, False, True, False, False], dtype=bool)
>>> X[X>15]
array([51, 55, 19])

Python 等动态类型语言一般比 C 和 C++ 等静态类型语言（编译型语言）
运算速度慢。为此，当 Python 中追求性能时，人们会用 C/C++ 来实现
处理的内容。Python 则承担“中间人”的角色，负责调用那些用 C/
C++ 写的程序。NumPy 中，主要的处理也都是通过 C 或 C++ 实现的。
因此，我们可以在不损失性能的情况下，使用 Python 便利的语法。

1.4 Matplotlib

用于图形的绘制和数据的可视化

1.4.1 绘制简单图形

使用 matplotlib 的 pyplot 模块绘制图形。

  • 使用了 Numpy 的arange 方法为数组赋值

  • 将通过 sin，将一系列（x，y）传给plt.plot方法

  • 最后调用plt.show显示

1
2
3
4
5
6
7
8
import numpy as np
import matplotlib.pyplot as plt
# 生成数据
x = np.arange(0, 6, 0.1) # 以 0.1 为单位，生成 0 到 6 的数据
y = np.sin(x)
# 绘制图形
plt.plot(x, y)
plt.show()

![image.png](深度学习入门 + 前四章 +678689c2-468f-49f5-ba9d-fc832005bf72/image 4.png)

1.4.2 pyplot 的功能

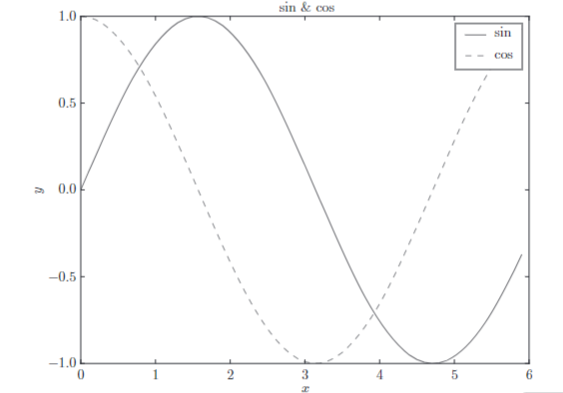
绘制 sin 和 cos 的图形，并使用 pyplot 的添加标题和轴标签等功能。

还是先用 np 生成数据，再用 plt.plot 绘图，通过添加参数 lable和linestyle 给图形添加标签、规定线条样式，然后用plt.xlabel和plt.ylabel确定 x、y 轴，用 plt.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np
import matplotlib.pyplot as plt
# 生成数据
x = np.arange(0, 6, 0.1) # 以 0.1 为单位，生成 0 到 6 的数据
y1 = np.sin(x)
y2 = np.cos(x)
# 绘制图形FS
plt.plot(x, y1, label="sin")
plt.plot(x, y2, linestyle = "--", label="cos") # 用虚线绘制
plt.xlabel("x") # x 轴标签
plt.ylabel("y") # y 轴标签
plt.title('sin & cos') # 标题
plt.legend()
plt.show()

image.png

1.4.3 显示图像

首先使用 matplotlib.image 模块的 imread() 方法读入图像,然后使用 pyplot 的 imshow() 显示图像。

1
2
3
4
5
import matplotlib.pyplot as plt
from matplotlib.image import imread # from ··· import ···
img = imread('lena.png') # 读入图像（设定合适的路径！）
plt.imshow(img)
plt.show()

image.png

这里，我们假定图像 lena.png 在当前目录下。读者根据自己的环境，可
能需要变更文件名或文件路径。另外，本书提供的源代码中，在 dataset 目
录下有样本图像 lena.png。比如，在通过 Python 解释器从 ch01 目录运行上
述代码的情况下，将图像的路径 ‘lena.png’ 改为 ‘../dataset/lena.png’，即
可正确运行。

相对路径中:
“./”：代表目前所在的目录
“. ./”：代表上一层目录
“/”：代表根目录

​

第二章 感知机

感知机 (perceptron) 这神经网络 (深度学习) 的起源算法

2.1 什么是感知机

感知机接收都多个信号,输出一个信号

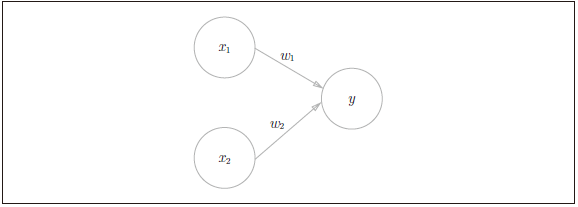
image.png

x1、x2 是输入信号，y 是输出信号，w1、w2 是权重（w 是 weight 的首字母）。图中的○称为“神经元”或者“节点”。输入信号被送往神经元时，会被分别乘以固定的权重，神经元会计算传送过来的信号的总和，只有当这个总和超过了某个界限值时，才会输出 1。这也称为“神经元被激活” 。这里将这个界限值称为阈值，用符号θ 表示
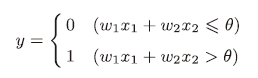
image.png

2.2 简单逻辑电路

2.2.1 与门

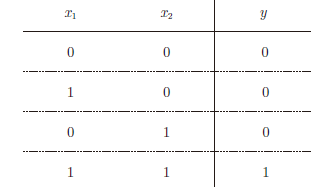
image.png

满足图 2-2 的条件的参数的选择方法有无数多个。比如，
当 (w1, w2, θ) = (0.5, 0.5, 0.7) 时，可以满足图 2-2 的条件。此外，当 (w1, w2, θ) 为 (0.5, 0.5, 0.8) 或者 (1.0, 1.0, 1.0) 时，同样也满足与门的条件。设定这样的参数后，仅当 x1 和 x2 同时为 1 时，信号的加权总和才会超过给定的阈值θ。

2.2.2 与非门和或非门

与非门 (NAND gate),即 Not AND,与门的反面,仅当 x1 和 x2 同时为 1 时输出 0,其他时候输出 1。要表示与非门，可以用 (w1, w2, θ) = (−0.5, −0.5, −0.7) 这样的组合（其
他的组合也是无限存在的）。实际上，只要把实现与门的参数值的符号取反，就可以实现与非门。

或门是“只要有一个输入信号是 1，输出就为 1”的逻辑电路。可以用 (w1, w2, θ) = (0.7,0.7, 0.5) 这样的组合（其他的组合也是无限存在的）

实际机器学习呢,决定 (w1, w2, θ) 的工作交由计算机自动进行。学习是确定合适的参数的过程，而人要做的是思考感知机的构造（模型），并把训练数据交给计算机。

通过调整参数值，相同构造的感知机就可以变为各种逻辑门。

2.3 感知机的实现

2.3.1 简单的实现

1
2
3
4
5
6
7
  def AND(x1, x2):
 w1, w2, theta = 0.5, 0.5, 0.7   #初始化参数w1,w2,theta
 tmp = x1*w1 + x2*w2
 if tmp <= theta:
return 0
 elif tmp > theta:
return 1

2.3.2 导入权重和偏置

刚才的与门的实现比较直接、容易理解，但是考虑到以后的事情，我们将其修改为另外一种实现形式

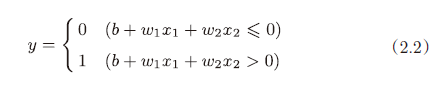
image.png

此处，b 称为偏置，w1 和 w2 称为权重。

1
2
3
4
5
6
7
8
9
10
>>> import numpy as np
>>> x = np.array([0, 1]) # 输入
>>> w = np.array([0.5, 0.5]) # 权重
>>> b = -0.7 # 偏置
>>> w*x
array([ 0. , 0.5])
>>> np.sum(w*x)
0.5
>>> np.sum(w*x) + b
-0.19999999999999996 # 大约为-0.2（由浮点小数造成的运算误差）

2.3.3 使用权重和偏置的实现

这里用偏置 b 替代−θ。

偏置和权重的作用是不同的：

  • 权重控制输入信号的重要性，
  • 而偏置调整神经元被激活的容易程度（输出信号为 1 的程度）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def AND(x1, x2):    # 与门
  x = np.array([x1, x2])
  w = np.array([0.5, 0.5])
  b = -0.7
  tmp = np.sum(w*x) + b
  if tmp <= 0:
	 return 0
  else:
	 return 1

def NAND(x1, x2):   #与非门
  x = np.array([x1, x2])
  w = np.array([-0.5, -0.5]) # 仅权重和偏置与AND不同！
  b = 0.7
  tmp = np.sum(w*x) + b
  if tmp <= 0:
	 return 0
  else:
	 return 1

def OR(x1, x2):#或门
  x = np.array([x1, x2])
  w = np.array([0.5, 0.5]) # 仅权重和偏置与AND不同！
  b = -0.2
  tmp = np.sum(w*x) + b
  if tmp <= 0:
	 return 0
  else:
	 return 1

2.4 感知机的局限性

2.4.1 异或门

感知机无法实现异或门

首先,将或门的动作形象化,当权重参数
(b, w1, w2) = (−0.5, 1.0, 1.0) 时，可满足图 2-4 的真值表条件。此时，感知机
可用下面的式（2.3）表示。

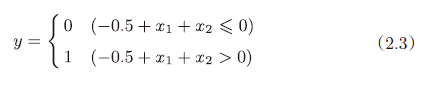
image.png

image.png

或门的四个结果以○和△表示，b+w1x1+w2x2 = 0 这条直线下方的 y=0,上方的 y=1，所以要实现或门，需要用直线将○和△分开。

但是,换成异或门就不行

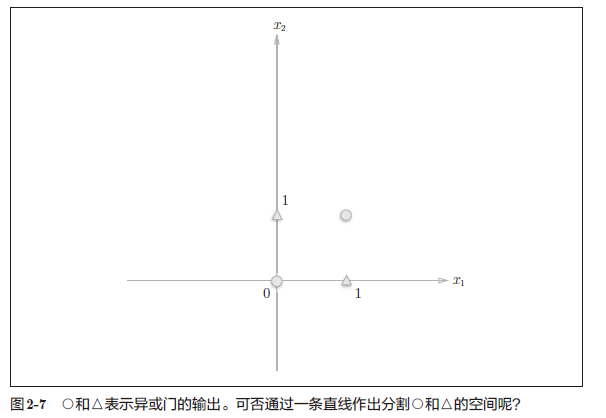
image.png

2.4.2　线性和非线性

感知机的局限性就在于它只能表示由一条直线分割的空间。图 2-8 这样弯
曲的曲线无法用感知机表示。另外，由图 2-8 这样的曲线分割而成的空间称为
非线性空间，由直线分割而成的空间称为线性空间。

image.png

2.5 多层感知机

2.5.1 已有门电路的组合

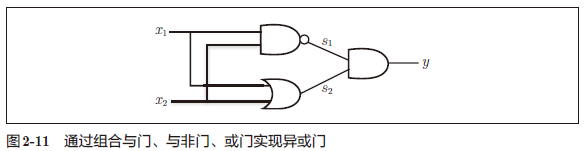
image.png

2.5.2 异或门的实现

1
2
3
4
5
 def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y

如图 2-13 所示，异或门是一种多层结构的神经网络。这里，将最左边的
一列称为第 0 层，中间的一列称为第 1 层，最右边的一列称为第 2 层。

image.png

实际上，与门、或门是单层感知机，而异或门是 2 层感知机。叠加了多
层的感知机也称为多层感知机（multi-layered perceptron）。

图 2-13 中的感知机总共由 3 层构成，但是因为拥有权重的层实质
上只有 2 层（第 0 层和第 1 层之间，第 1 层和第 2 层之间），所以称
为“2 层感知机”。

具体是像流水线组装作业一样的过程：

  1. 第 0 层的两个神经元接收输入信号，并将信号发送至第 1 层的神经元。

  2. 第 1 层的神经元将信号发送至第 2 层的神经元，第 2 层的神经元输出 y。

通过这样的结构（2 层结构），感知机得以实现异或门。这可以解释为“单层感知机无法表示的东西，通过增加一层就可以解决”。也就是说，通过叠加层（加深层），感知机能进行更加灵活的表示。

2.6 从与非门到计算机

计算机最底层是由逻辑电路组成的，计算机和感知机一样也有输入和输出,仅通过与非门的组合实现计算机是可行的。

理论上可以说 2 层感知机就能构建计算机。这是因为，已有研究证明，2 层感知机（严格地说是激活函数使用了非线性的 sigmoid 函数的感知机，具体请参照下一章）可以表示任意函数但是，使用 2 层感知机的构造，通过设定合适的权重来构建计算是一件非常累人的事情。实际上，在用与非门等低层的元件构建计算机的情况下，分阶段地制作所需的零件（模块）会比较自然，即先实现与门和或门，然后实现半加器和全加器，接着实现算数逻辑单元（ALU），然后实现 CPU。因此，通过感知机表示计算机时，使用叠加了多层的构造来实现是比较自然的流程。

第三章 神经网络

神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。

3.1 从感知机到神经网络

3.1.1 神经网络的例子

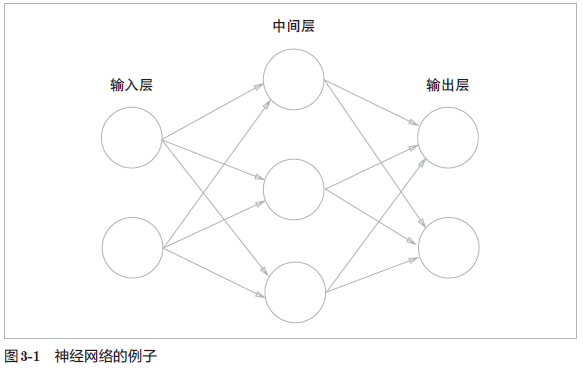
image.png

最左边叫输入层，最右边叫输出层，中间的一列叫中间层。中间层也称隐藏层，隐藏层的神经元（和输入层、输出层不同）肉眼看不见。输入层为第 0 层。

图 3-1 中的网络一共由 3 层神经元构成，但实质上只有 2 层神经元有权重，因此将其称为“2 层网络”。

3.1.2 复习感知机

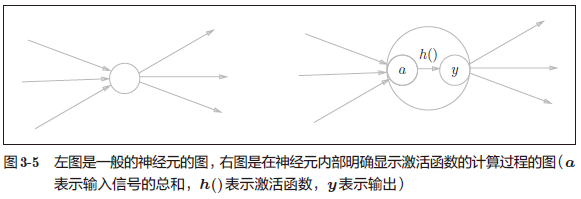
把偏置 b 给画出来了，由于偏置的输入信号一直是 1，所以为了区别于其他神经元，我们在图中把这个神经元整个涂成灰色。

image.png

现将式子简化，用一个函数来表示这种分情况的动作（超过 0 则输出 1，否则输出 0）。引入新函数 h(x)

$y = h\cdot(b + w_{1}x_{1} + w_{2}x_{2})$ (3.2)

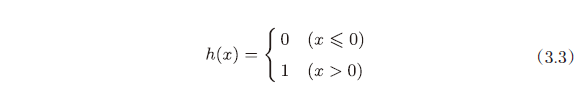
image.png

3.1.3 激活函数登场

将 h(x) 函数这样会将输入信号的总和转换为输出信号的函数一般称为激活函数（activation function）。激活函数的作用在于决定如何来激活输入信号的总和。

进一步改写式（3.2）。式（3.2）分两个阶段进行处理，先计算输入
信号的加权总和，然后用激活函数转换这一总和。

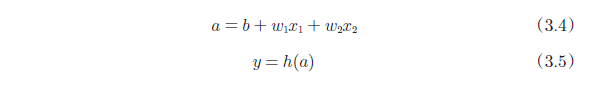
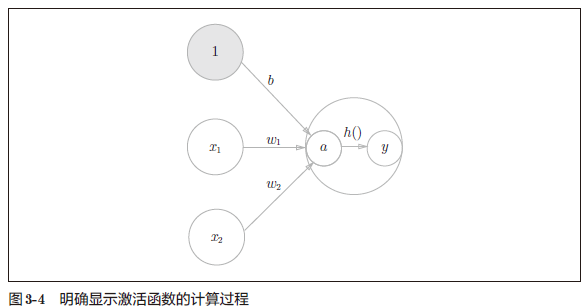
image.png

image.png

image.png

“朴素感知机”是指单层网络，指的是激活函数使用了阶跃函数的模型。“多层感知机”是指神经网络，即使用 sigmoid 函数（后述）等平滑的激活函数的多层网络

3.2 激活函数

式（3.3）的感知机用的阶跃函数，如果将激活函数从阶跃函数换成其他函数，就可以进入神经网络的世界了。

3.2.1 sigmoid 函数

sigmoid 函数：

$h(x)=\frac{1}{1+e^{-x}} —(3.6)$

3.2.2 阶跃函数的实现

1
2
3
4
5
def step_function(x):
  if x > 0:
 return 1
  else:
 return 0

但是参数 x 只能接受实数（浮点数），不允许参数取 NumPy 数组。改进以使其可以数组为参数。

1
2
3
 def step_function(x):
y = x > 0
return y.astype(np.int)

1
2
3
4
5
6
7
8
9
10
>>> import numpy as np
>>> x = np.array([-1.0, 1.0, 2.0])
>>> x
array([-1., 1., 2.])
>>> y = x > 0   # 对数组x进行不等号运算，生成一个布尔型数组y
>>> y
array([False, True, True], dtype=bool)
>>> y = y.astype(np.int)    # 阶跃函数返回的是int，所以需要把bool转为int
>>> y
array([0, 1, 1])

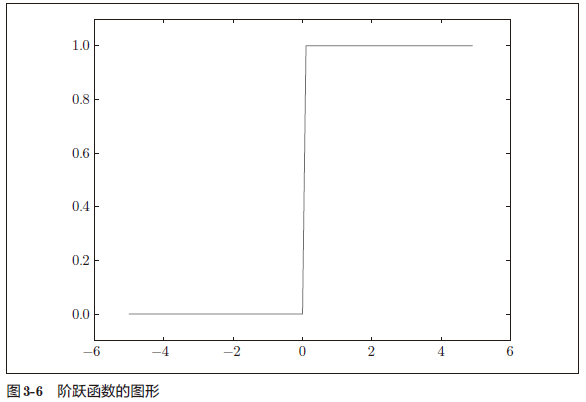
3.2.3 阶跃函数的图形

1
2
3
4
5
6
7
8
9
10
11
 import numpy as np
 import matplotlib.pylab as plt
 
 def step_function(x):
return np.array(x > 0, dtype=np.int) 

 x = np.arange(-5.0, 5.0, 0.1)  # 以0.1为单位,在[-5.0,5.0)生成数组
 y = step_function(x)
 plt.plot(x, y)
 plt.ylim(-0.1, 1.1) # 指定y轴的范围
 plt.show()

image.png

3.2.4 sigmoid 函数的实现

1
2
3
4
5
6
 def sigmoid(x):
return 1 / (1 + np.exp(-x))

 >>> x = np.array([-1.0, 1.0, 2.0])
 >>> sigmoid(x)
 array([ 0.26894142, 0.73105858, 0.88079708])    # NumPy的广播功能

画图的代码同上 (图见 3-7)

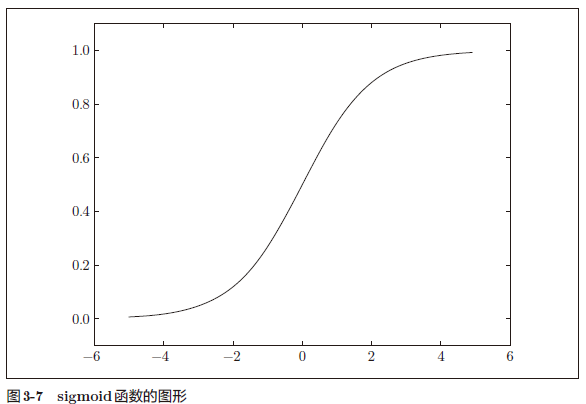
image.png

3.2.5 sigmoid 函数和阶跃函数的比较

不同：

  • 随着输入，一个输出平滑变化，一个输出急剧变化

  • 感知机中神经元之间流动的是 0 或 1 的二元信号，而神经网络中流动的是连续
    的实数值信号。（和刚才的平滑性有关）
    相同：

  • “输入小时，输出接近 0（为 0）；随着输入增大，输出向 1 靠近（变成 1）”

  • 不管输入信号有多小，或者有多大，输出信号的值都在 0 到 1 之间。

3.2.6 非线性函数

sigmoid 函数和阶跃函数还有一个共同点，就是两者都是非线性函数。
神经网络的激活函数必须使用非线性函数。换句话说，激活函数不能使用线性函数。
线性函数的问题在于，不管如何加深层数，总是存在与之等效的“无隐藏层的神经网络”：

把 y(x) = h(h(h(x))) 的运算对应 3 层神经网络 A。这个运算会进行
y(x) = c × c × c × x 的乘法运算，但是同样的处理可以由 y(x) = ax（注意，
a = $c^3$）这一次乘法运算（即没有隐藏层的神经网络）来表示。

使用线性函数时，无法发挥多层网络带来的优势。

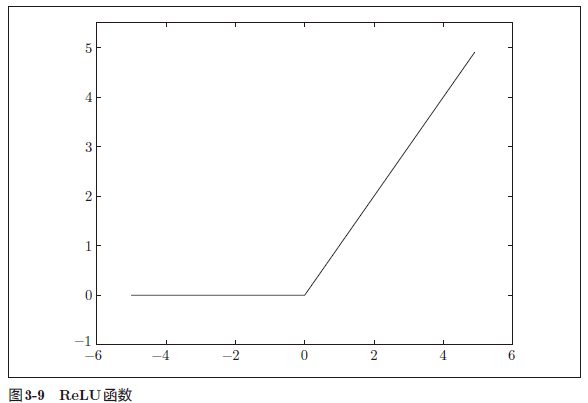
3.2.7 ReLU 函数

在神经网络发展的历史上，sigmoid 函数很早就开始被使用了，而最近则主要
使用 ReLU（Rectified Linear Unit）函数。

ReLU 函数可以表示为下面的式 (3.7)。

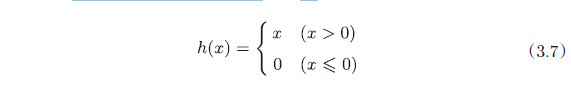
image.png

1
2
 def relu(x):
return np.maximum(0, x)

image.png

3.3 多维数组的运算

3.3.1 多维数组

1
2
3
4
5
6
7
8
9
10
>>> import numpy as np
>>> A = np.array([1, 2, 3, 4])
>>> print(A)
[1 2 3 4]
>>> np.ndim(A)  # 数组的维数可以通过np.dim()函数获得
1
>>> A.shape# 数组的形状可以通过实例变量shape获得
(4,)
>>> A.shape[0]
4

注意，这里的 A.shape 的结果是个元组（tuple）。这是因为一维数组的情况下也要返回和多维数组的情况下一致的结果。

1
2
3
4
5
6
7
8
9
>>> B = np.array([[1,2], [3,4], [5,6]])
>>> print(B)
[[1 2]
[3 4]
[5 6]]
>>> np.ndim(B)
2
>>> B.shape
(3, 2)

第一个维度有 3 个元素，第二个维度有 2 个元素。另外，第一个维度对应第 0 维，第二个维度对应第 1 维（Python 的索引从 0 开始）

3.3.2 矩阵乘法

1
2
3
4
5
6
7
8
9
   >>> A = np.array([[1,2], [3,4]])
   >>> A.shape
   (2, 2)
   >>> B = np.array([[5,6], [7,8]])
   >>> B.shape
   (2, 2)
   >>> np.dot(A, B)    # dot(A,B) 和dot(B,A)可不同, 向量运算注意顺序
   array([[19, 22],
[43, 50]])

它们的乘积可以通过 NumPy 的**np.dot()**函数计算（乘积也称为点积）。np.dot() 接收两个 NumPy 数组作为参数，并返回数组的乘积。

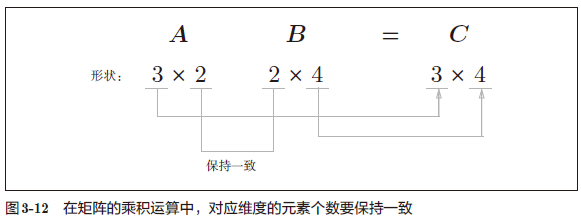
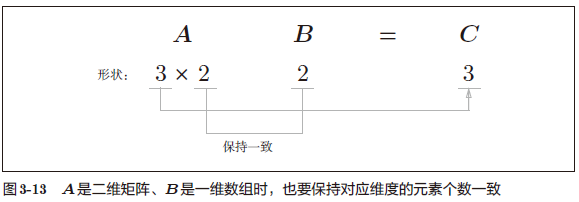
这里需要注意的是矩阵的形状（shape）。

1
2
3
4
5
6
7
8
9
   >>> C = np.array([[1,2], [3,4]])
   >>> C.shape
   (2, 2)
   >>> A.shape
   (2, 3)
   >>> np.dot(A, C)
   Traceback (most recent call last):
File "<stdin>", line 1, in <module>
   ValueError: shapes (2,3) and (2,2) not aligned: 3 (dim 1) != 2 (dim 0)

矩阵 A 的第 1 维的元素个数（列数）必须和矩阵 B 的第 0 维的元素个数（行数）相等

还有一点很重要，就是运算结果的矩阵 C 的形状是由矩阵 A 的行数和矩阵 B 的列数构成的。

image.png

image.png

3.3.3 神经网络的内积

下面我们使用 NumPy 矩阵来实现神经网络。这里我们以图 3-14 中的简
单神经网络为对象。这个神经网络省略了偏置和激活函数，只有权重。

image.png

1
2
3
4
5
6
7
8
9
10
11
12
>>> X = np.array([1, 2])
>>> X.shape
(2,)
>>> W = np.array([[1, 3, 5], [2, 4, 6]])
>>> print(W)
[[1 3 5]
 [2 4 6]]
>>> W.shape
(2, 3)
>>> Y = np.dot(X, W)
>>> print(Y)
[ 5 11 17]

如上所示，使用 np.dot（多维数组的点积），可以一次性计算出 Y 的结果。

3.4 3 层神经网络的实现

以图 3-15 的 3 层神经网络为对象，实现从输入到输出的（前向）处理。
在代码实现方面，使用上一节介绍的 NumPy 多维数组。巧妙地使用 NumPy 数组，可以用很少的代码完成神经网络的前向处理。

image.png

3.4.1 符号确认

本节的重点是神经网络的运算可以作为矩阵运算打包进行。因为神经网络各层的运算是通过矩阵的乘法运算打包进行的（从宏观视角来考虑），所以即便忘了（未记忆）具体的符号规则，也不影响理解后面的内容。

image.png

3.4.2 各层间信号传递的实现

  • 从输入层到第 1 层的第 1 个神经元的信号传递过程

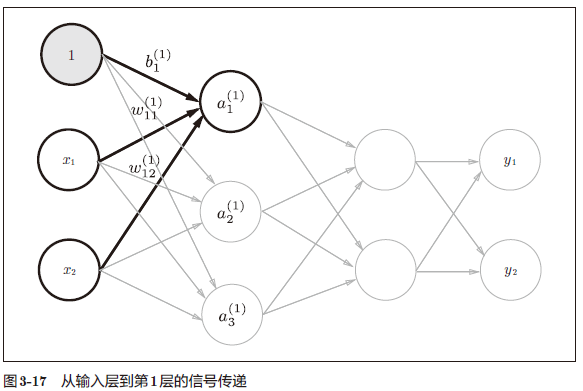
image.png

图 3-17 中增加了表示偏置的神经元“1”。请注意，偏置的右下角的索引号只有一个。这是因为前一层的偏置神经元（神经元“1”）只有一个

任何前一层的偏置神经元“1”都只有一个。偏置权重的数量取决于后一层的神经元的数量（不包括后一层的偏置神经元“1”）

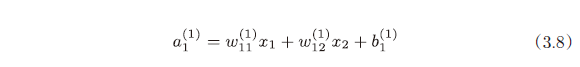
image.png

用矩阵表示就是：

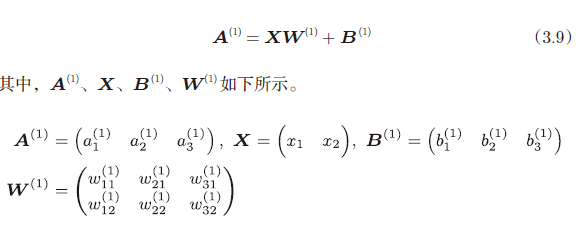
image.png

1
2
3
4
5
6
7
8
9
X = np.array([1.0, 0.5])
W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])

print(W1.shape) # (2, 3)
print(X.shape) # (2,)
print(B1.shape) # (3,)

A1 = np.dot(X, W1) + B1
  • 接下来，我们观察第 1 层中激活函数的计算过程。。

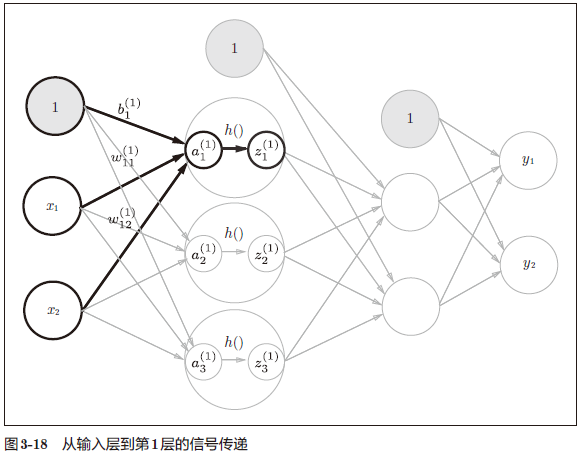
image.png

1
2
3
4
Z1 = sigmoid(A1)    # 激活函数采用sigmoid

print(A1) # [0.3, 0.7, 1.1]
print(Z1) # [0.57444252, 0.66818777, 0.75026011]
  • 下面，我们来实现第 1 层到第 2 层的信号传递（图 3-19）。

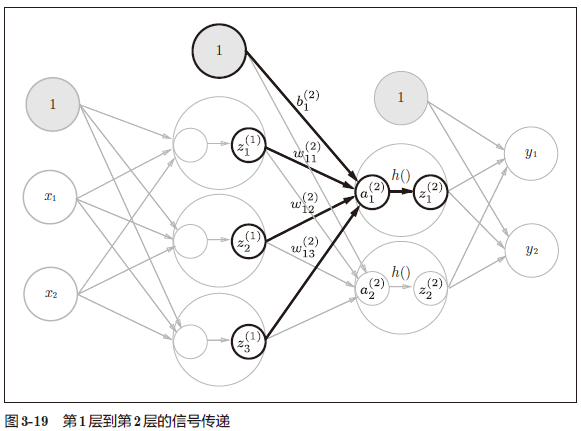
image.png

1
2
3
4
5
6
7
8
9
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])

print(Z1.shape) # (3,)
print(W2.shape) # (3, 2)
print(B2.shape) # (2,)

A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)
  • 最后是第 2 层到输出层的信号传递（图 3-20）。

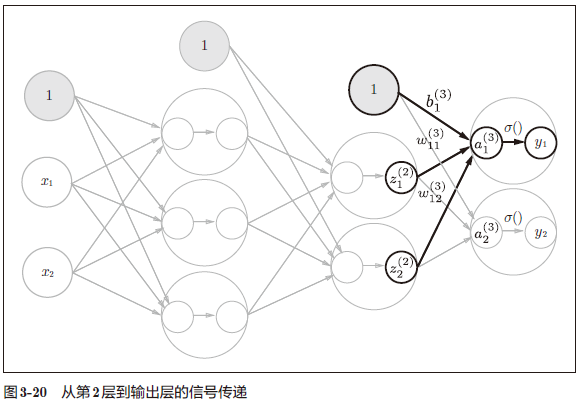
image.png

1
2
3
4
5
6
7
8
 def identity_function(x): # 恒等函数
return x
   
 W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
 B3 = np.array([0.1, 0.2])
 
 A3 = np.dot(Z2, W3) + B3
 Y = identity_function(A3) # 或者Y = A3

3.4.3 代码实现小结

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
 def init_network():
network = {} # 字典变量
network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
network['b1'] = np.array([0.1, 0.2, 0.3])
network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
network['b2'] = np.array([0.1, 0.2])
network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
network['b3'] = np.array([0.1, 0.2])

return network

 def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']

a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = identity_function(a3)

return y 

 network = init_network()
 x = np.array([1.0, 0.5])
 y = forward(network, x)
 print(y) # [ 0.31682708 0.69627909]

3.5 输出层的设计

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言，回归问题用恒等函数，分类问题用 softmax 函数。
分类问题是数据属于哪一个类别的问题。比如，区分图像中的人是男性还是女性
的问题就是分类问题。
而回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就是回归问题（类似“57.4kg”这样的预测）。

3.5.1 恒等函数和 softmax 函数

恒等函数会将输入按原样输出，对于输入的信息，不加以任何改动地直接输出。

image.png

分类问题中使用的softmax 函数：

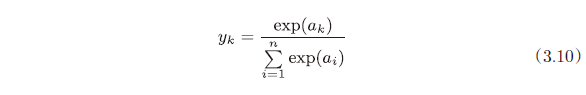
image.png

该式表示假设输出层共有 n 个神经元，计算第 k 个神经元的输出$y_{k}$。分子是输入信号**$a_{k}$**的指数函数，分母是所有输入信号的指数函数的和。

图 3-22 中，softmax 函数的输出通过箭头与所有的输入信号相连。这是因为，从式（3.10）可以看出，输出层的各个神经元都受到所有输入信号的影响。

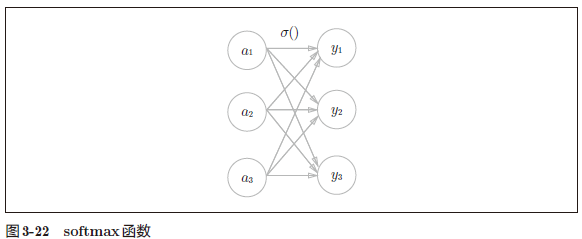
image.png

1
2
3
4
5
6
 def softmax(a):
exp_a = np.exp(a)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a

return y

3.5.2 实现 softmax 函数时的注意事项

上面的 softmax 函数的实现虽然正确描述了式（3.10），但在计算机的运算上有一定的缺陷。这个缺陷就是溢出问题。

比如，$e^{10}$ 的值会超过 20000，$e^{100}$ 会变成一个后面有 40 多个 0 的超大值，$e^{1000}$ 的结果会返回一个表示无穷大的 inf。如果在这些超大值之间进行除法运算，结果会出现“不确定”的情况。

softmax 函数的实现可以像式（3.11）这样进行改进。

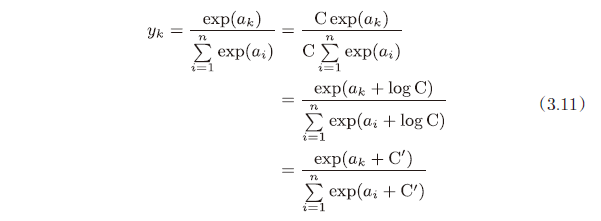
image.png

首先，在分子和分母上都乘上 C 这个任意的常数。然后，把这个 C 移动到
指数函数（exp）中，记为 log C。最后，把 log C 替换为另一个符号 C’ 。

这里的 C’ 可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。

1
2
3
4
5
6
7
 def softmax(a):
c = np.max(a)   # 取输入信号的最大值
exp_a = np.exp(a - c) # 溢出对策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a

return y

3.5.3 softmax 函数的特征

softmax 函数的输出是 0.0 到 1.0 之间的实数。并且，softmax 函数的输出值的总和是 1。因此，我们把 softmax 函数的输出解释为“概率”。

使用了 softmax 函数，各个元素之间的大小关系也不会改变

一般而言，神经网络只把输出值最大的神经元所对应的类别作为识别结果。因此，一般不会在输出层使用 softmax 函数。

求解机器学习问题的步骤可以分为“学习”和“推理”两个阶段。“学习”也称为“训练”，是指使用训练数据、自动调整参数的过程。在推理阶段，用学到的模型对未知的数据进行推理（分类）

3.5.4 输出层的神经元数量

输出层的神经元数量需要根据待解决的问题来决定。对于分类问题，输
出层的神经元数量一般设定为类别的数量。

3.6 手写数字识别

这里我们来进行手写数字图像的分类。假设学习已经全部结束，我们使用学习到的参数，先实现神经网络的“推理处理”。这个推理处理也称为神经网络的前向传播（forward propagation）

3.6.1 MNIST 数据集

MNIST 手写数字图像集，机器学习领域最有名的数据集之一。

不能跨目录导入文件，需要跨目录的话，使用 sys.path.append(路径) 语句
如:sys.path.append(os.pardir) 语句，把父目录加入到 sys.path（Python 的搜索模块的路径集）中，从而可以导入父目录下任何目录（包括 dataset 目录）中的任何文件

Python 的 pickle 功能：可以将程序运行中的对象保存为文件。如果加载保存过的 pickle 文件，可以立刻复原之前程序运行中的对象。（在第 2 次及以后读入时，读入 MNIST 数据集的 load_mnist() 函数内部也使用了 pickle 功能）

load_mnist 函数以“( 训练图像, 训练标签)，( 测试图像，测试标签)”的形式返回读入的 MNIST 数据。

load_mnist(normalize=True,flatten=True, one_hot_label=False)

  • normalize：是否将输入图像正规化为 0.0～1.0 的值（为 False，则输入图像的像素会保持原来的 0～255）

  • flatten：是否展开输入图像（变成一维数组）（为 False，则输入图像为 1 × 28 × 28 的三维数组；为 True，则输入图像会保存为由 784 个元素构成的一维数组。）

  • one_hot_label：是否将标签保存为 one-hot 表示（one-hot representa-tion）。one-hot 表示是仅正确解标签为 1，其余皆为 0 的数组，就像 [0,0,1,0,0,0,0,0,0,0] 这样。（为 False，是像 7、2 这样简单保存正确解标签）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
 # coding: utf-8
 import sys, os
 sys.path.append('.')  # 为了导入父目录的文件而进行的设定
 import numpy as np
 from dataset.mnist import load_mnist
 from PIL import Image
 
 print(os.pardir)
 
 def img_show(img):
pil_img = Image.fromarray(np.uint8(img))    
pil_img.show()
 
 (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
 
 img = x_train[0]
 label = t_train[0]
 print(label)  # 5
 
 print(img.shape)  # (784,)
 img = img.reshape(28, 28)  # 把图像的形状变为原来的尺寸
 print(img.shape)  # (28, 28)
 
 img_show(img)

os.pardir 的值是 ‘..’，一个 ‘.’ 意为返回上一级目录，所以使用 os.pardir 时注意检查命令行所在目录级。（命令行目录级和运行的程序级中间可以隔一级）

flatten=True 时读入的图像是以一列（一维）NumPy 数组的形式保存的。因此，显示图像时，需要用 reshape() 它变为原来的 28 像素× 28 像素的形状。

PIL 模块 (pillow) 负责图像显示，需要把保存为 NumPy 数组的图像数据转换为 PIL 用
的数据对象，这个转换处理由 Image.fromarray() 来完成

3.6.2 神经网络的推理处理

神经网络的输入层有 28 × 28 = 784 个神经元，输出层有 0 到 9，共 10 个神经元。
此外，这个神经网络有 2 个隐藏层，第 1 个隐藏层有 50 个神经元，第 2 个隐藏层有 100 个神经元。这个 50 和 100 可以设置为任何值。

1
2
3
 def get_data():
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test

将 normalize 设置成 True 后，函数内部会进行转换，将图像的各个像素值除以 255，使得数据的值在 0.0～1.0 的范围内。像这样把数据限定到某个范围内的处理称为正规化（normalization）。此外，对神经网络的输入数据进行某种既定的转换称为预处理（pre-processing）。这里，作为对输入图像的一种预处理，我们进行了正规化。

1
2
3
4
  def init_network():
 with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
 return network
1
2
3
4
5
6
7
8
9
10
11
12
 def predict(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
 
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = softmax(a3)
 
return y
1
2
3
4
5
6
7
8
9
10
  x, t = get_data()
  network = init_network()
  accuracy_cnt = 0
  for i in range(len(x)):# range返回的是一个整数列
 y = predict(network, x[i])  # 以NumPy数组的形式输出各个标签对应的概率。
 p= np.argmax(y) # 获取概率最高的元素的索引
 if p == t[i]:
accuracy_cnt += 1
  
  print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

首先获得 MNIST 数据集，生成网络。

接着，用 for 语句逐一取出保存在 x 中的图像数据，用 predict() 函数进行分类

最后，比较神经网络所预测的答案和正确解标签，将回答正确的概率作为识别精度。

3.6.3 批处理

以上就是处理 MNIST 数据集的神经网络的实现，现在我们来关注输入数据和权重参数的“形状”。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
>>> x, _ = get_data()   
>>> network = init_network()
>>> W1, W2, W3 = network['W1'], network['W2'], network['W3'] # 省略了偏置
>>>
>>> x.shape
(10000, 784)
>>> x[0].shape
(784,)
>>> W1.shape
(784, 50)
>>> W2.shape
(50, 100)
>>> W3.shape
(100, 10)

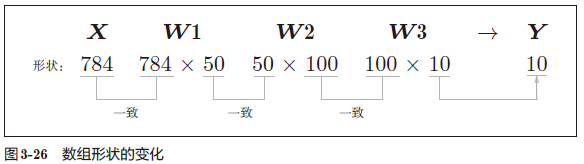
image.png

这是只输入一张图像数据时的处理流程。

现在我们来考虑打包输入多张图像的情形，比如一次性处理 100 张，可以把 x 的形状改为 100 × 784，输出数据的形状变为 100 × 10

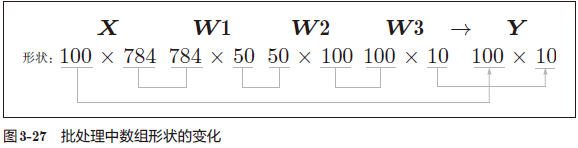
image.png

x[0] 和 y[0] 中保存了第 0 张图像及其推理结果，x[1] 和 y[1] 中保存了第 1 张图像及
其推理结果，等等。

这种打包式的输入数据称为批（batch）。

批处理对计算机的运算大有利处，可以大幅缩短每张图像的处理时间。批处理一次性计算大型数组要比分开逐步计算各个小型数组速度更快。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
 x, t = get_data()
 network = init_network()
 
 batch_size = 100 # 批数量
 accuracy_cnt = 0
 
 for i in range(0, len(x), batch_size):  # 设置步长为batch_size
x_batch = x[i:i+batch_size] # 取出从第i个到第i+batch_n个之间的数据。
y_batch = predict(network, x_batch)
p = np.argmax(y_batch, axis=1) # 指定沿着第1维方向(第二个维度,行方向)找
accuracy_cnt += np.sum(p == t[i:i+batch_size])
# 在NumPy数组之间使用比较运算符（==）生成布尔型数组，计算True的个数。
 print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
 
1
2
3
4
5
>>> x = np.array([[0.1, 0.8, 0.1], [0.3, 0.1, 0.6],
... [0.2, 0.5, 0.3], [0.8, 0.1, 0.1]])
>>> y = np.argmax(x, axis=1)
>>> print(y)
[1 2 1 0]

第四章 神经网络的学习

4.1 从数据中学习

4.1.1 数据驱动

一种方案是，先从图像中提取特征量，再用机器学习技术学习这些特征量的模式。这里所说的“特征量”是指可以从输入数据（输入图像）中准确地提取本质数据（重要的数据）的转换器。

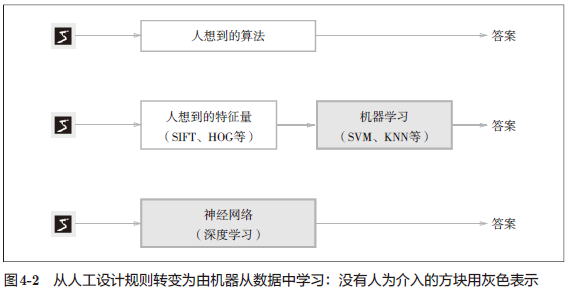
image.png

深度学习有时也称为端到端机器学习（end-to-end machinelearning）。这里所说的端到端是指从一端到另一端的意思，也就是从原始数据（输入）中获得目标结果（输出）的意思。

神经网络的优点是对所有的问题都可以用同样的流程来解决。比如，不管要求解的问题是识别 5，还是识别狗，抑或是识别人脸，神经网络都是通过不断地学习所提供的数据，尝试发现待求解的问题的模式。

4.1.2 训练数据和测试数据

数据分为训练数据和测试数据，首先，使用训练数据进行学习，寻找最优的参数；然后，使用测试数据评价训练得到的模型的实际能力。
训练数据也可以称为监督数据。

泛化能力是指处理未被观察过的数据（不包含在训练数据中的数据）的能力。获得泛化能力是机器学习的最终目标。

只对某个数据集过度拟合的状态称为过拟合（over fitting）。避免过拟合也是机器学习的一个重要课题。

4.2 损失函数

神经网络以某个指标为线索寻找最优权重参数。神经网络的学习中所用的指标称为损失函数（loss function）。这个损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。

损失函数是表示神经网络性能的“恶劣程度”的指标，即当前的神经网络对监督数据在多大程度上不拟合，在多大程度上不一致。加个负号就是“性能有多好”了。

4.2.1 均方误差

均方误差如下式所示。

image.png

$y_{k} $ 是表示神经网络的输出，$t_{k} $ 表示监督数据，$k $ 表示数据的维数。

1
2
 def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)   # 用"**2"表示2次方

4.2.2 交叉熵误差

交叉熵误差如下式所示。

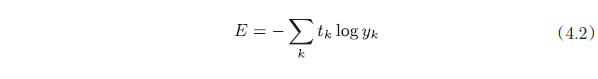
image.png

log 表示以 e 为底数的自然对数（$log_{e}$）jh $t_{k} $ 中只有正确解标签的索引为 1，其他均为 0（one-hot 表示）。因此，式（4.2）实际上只计算对应正确解标签的输出的自然对数。

1
2
3
 def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))

当出现 np.log(0) 时，np.log(0) 会变为负无限大的 -inf，这样一来就会导致后续计算无法进行。作为保护性对策，添加一个微小值 delta 可以防止负无限大的发生。

4.2.3 mini-batch 学习

前面介绍的损失函数的例子中考虑的都是针对单个数据的损失函数。如果要求所有训练数据的损失函数的总和，以交叉熵误差为例，可以写成下面的式（4.3）。

image.png

这里, 假设数据有 $N$ 个，$t_{nk}$ 表示第 n 个数据的第 $k $ 个元素的值（$y_{nk}$ 是神经网络的输出，$t_{nk}$ 是监督数据）。通过除以 N，可以求单个数据的“平均损失函数”。通过这样的平均化，可以获得和训练数据的数量无关的统一指标。

遇到大数据，百万级千万级的数据，这种情况下以全部数据为对象计算损失函
数是不现实的。因此，我们从全部数据中选出一部分，作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据（称为 mini-batch, 小批量），然后对每个 mini-batch 进行学习。这种学习方式叫mini-batch 学习。

1
2
3
4
5
6
7
8
9
10
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]

# np.random.choice()可以从指定的数字中随机选择想要的数
>>> np.random.choice(60000, 10)
array([ 8013, 14666, 58210, 23832, 52091, 10153, 8107, 19410, 27260,
21411])

4.2.4 mini-batch 版交叉熵误差的实现

1
2
3
4
5
6
7
  def cross_entropy_error(y, t):  # y是神经网络的输出,t是监督数据
 if y.ndim == 1:# y的维度为1表示求单个数据的交叉熵误差
t = t.reshape(1, t.size)    # 需要改变数据形状
y = y.reshape(1, y.size)

 batch_size = y.shape[0] # 要用batch 的个数进行正规化，计算单个数据的平均交叉熵误差。
 return -np.sum(t * np.log(y + 1e-7)) / batch_size
1
2
3
4
5
6
7
  def cross_entropy_error(y, t):
 if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)

 batch_size = y.shape[0]
 return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

由于 one-hot 表示中 t 为 0 的元素的交叉熵误差也为 0，因此针对这些元素的计算可以忽略。换言之，获得神经网络在正确解标签处的输出，就可以计算交叉熵误差。

y 是模型的输出，它是一个 (batch_size, num_classes) 的数组，其中 batch_size 是批量大小，num_classes 是类别数；
np.arange(batch_size) 生成一个包含 0 到 batch_size-1 的数组，用于索引 y 和 t；
y[np.arange(batch_size), t] 是一个包含每个样本对应类别概率的数组。它通过索引 y 的第一维和 t 的元素来获取。

比如，当 batch_size 为 5 时，np.arange(batch_size) 会生成一个 NumPy 数组 [0, 1, 2, 3, 4]。t 中标签是以 [2, 7, 0, 9, 4] 的形式存储的，y[np.arange(batch_size), t] 会生成 NumPy 数组 [y[0,2], y[1,7], y[2,0],y[3,9], y[4,4]]）。

4.2.5 为何要设定损失函数

对某一权重参数的损失函数求导，表示的是“如果稍微改变这个权重参数的值，损失函数的值会如何变化”。如果导数的值为负，通过使该权重参数向正方向改变，可以减小损失函数的值；反过来，如果导数的值为正，则通过使该权重参数向负方向改变，可以减小损失函数的值。

在进行神经网络的学习时，不能将识别精度作为指标。因为如果以识别精度为指标，则参数的导数在绝大多数地方都会变为 0。

识别精度对微小的参数变化基本上没有什么反应，即便有反应，它的值
也是不连续地、突然地变化。作为激活函数的阶跃函数也有同样的情况。出
于相同的原因，如果使用阶跃函数作为激活函数，神经网络的学习将无法进行。

4.3 数值微分

4.3.1 导数

导数的定义。
image.png

1
2
3
 def numerical_diff(f, x):
h = 10e-50
return (f(x+h) - f(x)) / h

数值微分的英文 numerical differentiation

在上面的实现中，因为想把尽可能小的值赋给 h（可以话，想让 h 无限接
近 0），所以 h 使用了 10e-50 这个微小值，但是，这样反而产生了舍入误差（rounding error），会导致小数的精细部分的数值被省略。

1
2
>>> np.float32(10e-50)
0.0

所以，第一个改进的地方就是即将微小值 h 改为 $10^{−4}$

第二个需要改进的地方与函数 f 的差分有关。

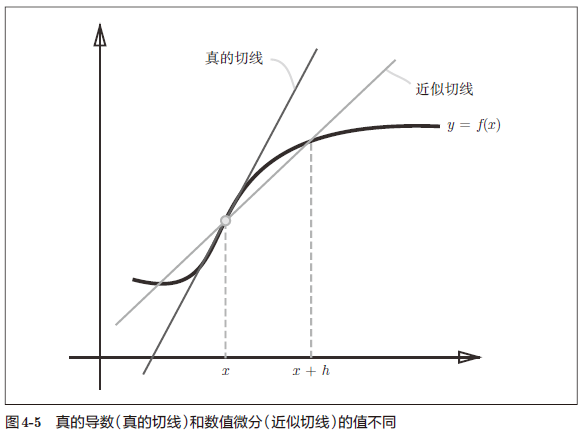
image.png

为了减小这个误差，改为计算函数 $f $ 在 $(x + h) $ 和 $(x − h) $ 之间的差分，这也被称为中心误差，而 (x+h) 和 x 之间的差分被称为前向差分。

1
2
3
 def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x+h) - f(x-h)) / (2*h)

利用微小的差分求导数的过程称为数值微分（numerical differentiation）。而基于数学式的推导求导数的过程，则用“解析性”（analytic）一词，称为“解析性求解”或者“解析性求导”

4.3.2 数值微分的例子

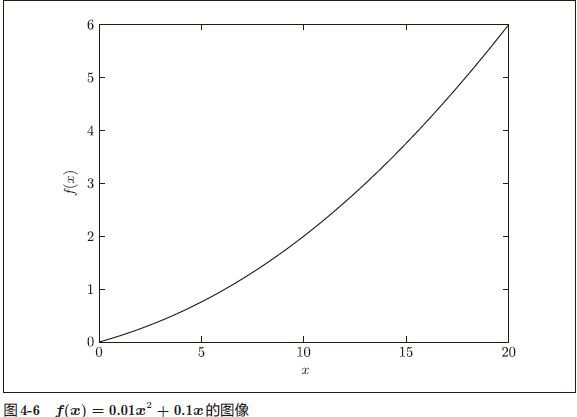
一个二次函数

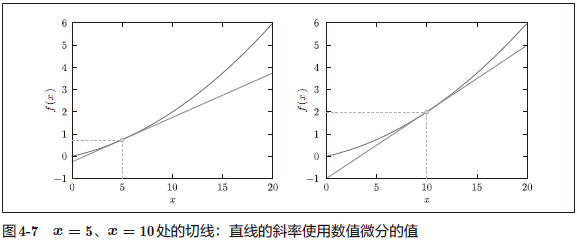
image.png

1
2
def function_1(x):
return 0.01*x**2 + 0.1*x

绘制图像

1
2
3
4
5
6
7
8
9
import numpy as np
import matplotlib.pylab as plt

x = np.arange(0.0, 20.0, 0.1) # 以0.1为单位，从0到20的数组x
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x, y)
plt.show()

image.png

计算函数在 x = 5 和 x = 10 处的导数。

1
2
3
4
>>> numerical_diff(function_1, 5)
0.1999999999990898  # 真的导数: 0.2
>>> numerical_diff(function_1, 10)  # 真的导数: 0.3
0.2999999999986347

用上面数值微分的值作斜率画直线

image.png

4.3.3 偏导数

函数有两个变量

函数

image.png

1
2
3
 def function_2(x): # 参数为一个Numpy数组
return x[0]**2 + x[1]**2
 # 或者return np.sum(x**2)

绘图
image.png

求偏导

问题 1：求 x0 = 3, x1 = 4 时，关于 x0 的偏导数。

1
2
3
4
5
>>> def function_tmp1(x0):
...return x0*x0 + 4.0**2.0 # 固定x1=4.0
...
>>> numerical_diff(function_tmp1, 3.0)
6.00000000000378

问题 2：求 x0 = 3, x1 = 4 时，关于 x1 的偏导数。

1
2
3
4
5
>>> def function_tmp2(x1):
...return 3.0**2.0 + x1*x1 # 固定x0=3.0
...
>>> numerical_diff(function_tmp2, 4.0)
7.999999999999119

偏导数需要将多个变量中的某一个变量定为目标变量，并将其他变量固定为某个值。

4.4 梯度

像 $(\frac{\partial f}{\partial x_{0}},\frac{\partial f}{\partial x_{1}})$ 这样的由全部变量的偏导数汇总而成的向量称为梯度（gradient）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
  def numerical_gradient(f, x):
 h = 1e-4 # 0.0001
 grad = np.zeros_like(x) # 生成和x形状相同的数组
  
 for idx in range(x.size):
tmp_val = x[idx]
# f(x+h)的计算
x[idx] = tmp_val + h
fxh1 = f(x)

# f(x-h)的计算
x[idx] = tmp_val - h
fxh2 = f(x)

grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值

 return grad

np.zeros_like() 返回与指定数组具有相同形状和数据类型的数组，并且数组中的值都为 0。

1
2
3
4
5
6
>>> numerical_gradient(function_2, np.array([3.0, 4.0]))
array([ 6., 8.])
>>> numerical_gradient(function_2, np.array([0.0, 2.0]))
array([ 0., 4.])
>>> numerical_gradient(function_2, np.array([3.0, 0.0]))
array([ 6., 0.])

绘制元素值为负梯度的向量

Text
1
见ch04/gradient_2d.py

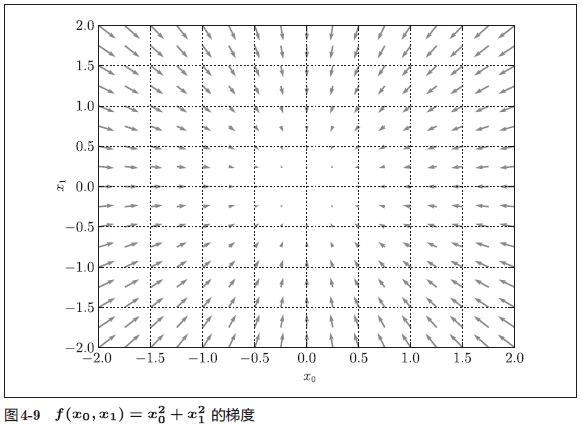
image.png

image.png

梯度的重要性质：梯度指示的方向是各点处的函数值减小最多的方向

梯度的本意是一个向量（矢量）， 表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。
(方向导数是函数沿任意方向求导所得函数，可由偏导数合成，因为偏导数是沿坐标轴求导)

直观理解梯度，以及偏导数、方向导数和法向量等 - shine-lee - 博客园

4.4.1 梯度法

一般而言，损失函数很复杂，参数空间庞大，我们不知道它在何处能取得最小值。而通过巧妙地使用梯度来寻找函数最小值（或者尽可能小的值）的方法就是梯度法。
这里需要注意的是，梯度表示的是各点处的函数值减小最多的方向。因此，无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。实际上，在复杂的函数中，梯度指示的方向基本上都不是函数值最小处。

函数的极小值、最小值以及被称为鞍点（saddle point）的地方，梯度为 0。极小值是局部最小值。
虽然梯度法是要寻找梯度为 0 的地方，但是那个地方不一定就是最小值（也有可能是极小值或者鞍点）。此外，当函数很复杂且呈扁平状时，学习可能会进入一个（几乎）平坦的地区，陷入被称为“学习高原”的无法前进的停滞期。

虽然梯度的方向并不一定指向最小值，但沿着它的方向能够最大限度地减小函数的值。

在梯度法中，函数的取值从当前位置沿着梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进，如此反复，不断地沿梯度方向前进。像这样，通过不断地沿梯度方向前进，逐渐减小函数值的过程就是梯度法（gradient method）。

寻找最小值的梯度法称为梯度下降法（gradient descent method），
寻找最大值的梯度法称为梯度上升法（gradient ascent method）。
但是通过反转损失函数的符号，求最小值的问题和求最大值的问题会变成相同的问题，因此“下降”还是“上升”的差异本质上并不重要。
一般来说，神经网络（深度学习）中，梯度法主要是指梯度下降法。

尝试用数学式来表示梯度法，如式（4.7）所示。

image.png

$η$ 表示更新量，在神经网络的学习中，称为学习率（learning rate）。学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数。

一般而言，这个值过大或过小，都无法抵达一个“好的位置”。在神经网络的学习中，一般会一边改变学习率的值，一边确认学习是否正确进行了。

1
2
3
4
5
6
7
8
  def gradient_descent(f, init_x, lr=0.01, step_num=100):
 x = init_x
  
 for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
  
 return x

参数 f 是要进行最优化的函数，init_x 是初始值，lr 是学习率 learning rate，step_num 是梯度法的重复次数。

使用这个函数可以求函数的极小值，顺利的话，还可以求函数的最小值。

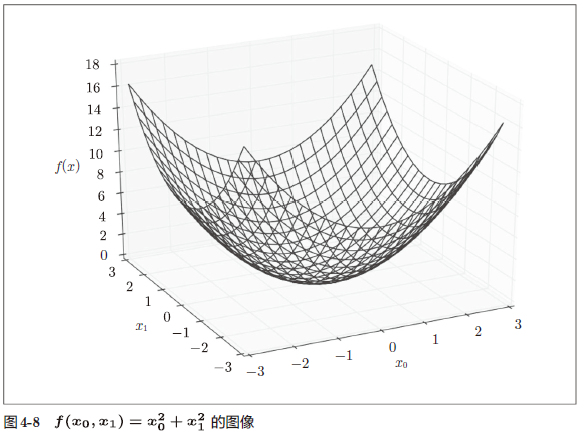
问题：请用梯度法求 $f(x_{0}+x_{1})=x_{0}^2+x_{1}^2$ 的最小值。

1
2
3
4
5
6
>>> def function_2(x):
... return x[0]**2 + x[1]**2
...
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)
array([ -6.11110793e-10, 8.14814391e-10])

最终的结果是 (-6.1e-10, 8.1e-10)，非常接近 (0，0)。实际上，真的最小值就是 (0，0)，所以说通过梯度法我们基本得到了正确结果。

1
2
3
4
5
6
7
8
9
# 学习率过大的例子：lr=10.0
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=10.0, step_num=100)
array([ -2.58983747e+13, -1.29524862e+12])

# 学习率过小的例子：lr=1e-10
>>> init_x = np.array([-3.0, 4.0])
>>> gradient_descent(function_2, init_x=init_x, lr=1e-10, step_num=100)
array([-2.99999994, 3.99999992])

实验结果表明，学习率过大的话，会发散成一个很大的值；反过来，学习率过小的话，基本上没怎么更新就结束了。

像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数，是人工设定的。一般来说，超参数需要尝试多个值，以便找到一种可以使学习顺利进行的设定。

4.4.2 神经网络的梯度

这里所说的梯度是指损失函数关于权重参数的梯度。
比如，有一个只有一个形状为 2 × 3 的权重 W 的神经网络，损失函数用 L 表示。

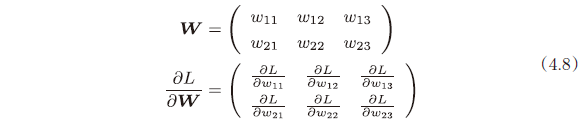
image.png

下面，以一个简单的神经网络为例，实现求梯度的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
  import sys, os
  sys.path.append(os.pardir)
  import numpy as np
  from common.functions import softmax, cross_entropy_error
  from common.gradient import numerical_gradient
  
  class simpleNet:
 def __init__(self):# 初始化权重
self.W = np.random.randn(2,3) # 用高斯分布进行初始化
  
 def predict(self, x):   # 输入与权重作内积
return np.dot(x, self.W)
  
 def loss(self, x, t):   # 损失函数使用交叉熵误差
z = self.predict(x)
y = softmax(z)  # 输出层的激活函数使用softmax
loss = cross_entropy_error(y, t)
  
return loss
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> net = simpleNet()
>>> print(net.W) # 权重参数
[[ 0.47355232 0.9977393 0.84668094],
[ 0.85557411 0.03563661 0.69422093]])
>>>
>>> x = np.array([0.6, 0.9])
>>> p = net.predict(x)
>>> print(p)
[ 1.05414809 0.63071653 1.1328074]
>>> np.argmax(p) # 最大值的索引
2
>>>
>>> t = np.array([0, 0, 1]) # 正确解标签
>>> net.loss(x, t)
0.92806853663411326
1
2
3
4
5
6
7
>>> def f(W):
...return net.loss(x, t)
...
>>> dW = numerical_gradient(f, net.W)
>>> print(dW)
[[ 0.21924763 0.14356247 -0.36281009]
[ 0.32887144 0.2153437 -0.54421514]]

（这里定义的函数 f(W) 的参数 W 是一个伪参数。因为 numerical_gradient(f,
x) 会在内部执行 f(x), 为了与之兼容而定义了 f(W)）。

观察一下 dW 的内容，例如，会发现 $\frac{\partial L}{\partial W}$ 中的 $\frac{\partial L}{\partial w_{11}}$ 的值大约是 0.2，这表示如果将 w11 增加 h，那么损失函数的值会增加 0.2h。再如，$\frac{\partial L}{\partial w_{23}}$ 对应的值大约是−0.5，这表示如果将 w23 增加 h，损失函数的值将减小 0.5h。

因此，从减小损失函数值的观点来看，w23 应向正方向更新，w11 应向负方向更新。至于更新的程度，w23 比 w11 的贡献要大。

在上面的代码中，定义新函数时使用了“def f(x):···”的形式。实际上，Python 中如果定义的是简单的函数，可以使用 lambda 表示法。

1
2
>>> f = lambda w: net.loss(x, t)
>>> dW = numerical_gradient(f, net.W)

4.5 学习算法的实现

神经网络的学习步骤如下所示。

前提
神经网络存在合适的权重和偏置，调整权重和偏置以便拟合训练数据的过程称为“学习”。神经网络的学习分成下面 4 个步骤。

步骤 1（mini-batch）
从训练数据中随机选出一部分数据，这部分数据称为 mini-batch。目标是减小 mini-batch 的损失函数的值。

步骤 2（计算梯度）
为了减小 mini-batch 的损失函数的值，需要求出各个权重参数的梯度。梯度表示损失函数的值减小最多的方向。

步骤 3（更新参数）
将权重参数沿梯度方向进行微小更新。

步骤 4（重复）
重复步骤 1、步骤 2、步骤 3。

不过因为这里使用的数据是随机选择的 mini batch 数据，所以又称为随机梯度下降法（stochastic gradient descent, SGD）

下面，我们来实现手写数字识别的神经网络。这里以 2 层神经网络（隐藏层为 1 层的网络）为对象，使用 MNIST 数据集进行学习。

4.5.1 2 层神经网络的类

1
2
源代码在ch04/two_layer_net.py
和上一章的神经网络的前向处理的实现有许多共通之处，所以并没有太多新东西

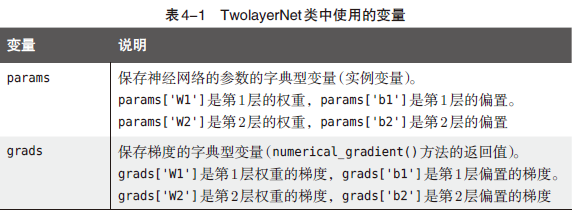
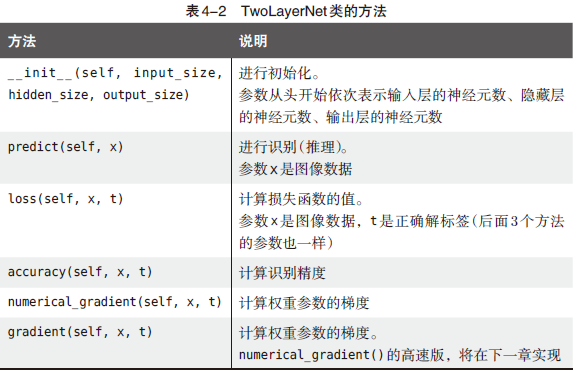
image.png

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
net = TwoLayerNet(input_size=784, hidden_size=100, output_size=10)
net.params['W1'].shape # (784, 100)
net.params['b1'].shape # (100,)
net.params['W2'].shape # (100, 10)
net.params['b2'].shape # (10,)

x = np.random.rand(100, 784) # 伪输入数据（100笔）
t = np.random.rand(100, 10) # 伪正确解标签（100笔）

grads = net.numerical_gradient(x, t) # 计算梯度

grads['W1'].shape # (784, 100)
grads['b1'].shape # (100,)
grads['W2'].shape # (100, 10)
grads['b2'].shape # (10,)

init(self,input_size, hidden_size, output_size) 方法

依次表示输入层的神经元数、隐藏层的神经元数、输出层的神经元数

输入图像的大小是 784（28 × 28），输出为 10 个类别，
所以指定参数 input_size=784、output_size=10，将隐藏层的个数 hidden_size
设置为一个合适的值即可。

此外，这个初始化方法会对权重参数进行初始化。

这里只需要知道，权重使用符合高斯分布的随机数进行初始化，偏置使用 0 进行初始化。

gradient(self, x, t)
是下一章要实现的方法，该方法使用误差反向传播法高效地计算梯度。

4.5.2 mini-batch 的实现

以 TwoLayerNet 类为对象，使用 MNIST 数据集进行学习（源代码在 ch04/train_
neuralnet.py 中）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
  import sys, os
  sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
  import numpy as np
  import matplotlib.pyplot as plt
  from dataset.mnist import load_mnist
  from two_layer_net import TwoLayerNet
  
  # 读入数据
  (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
  
  network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
  
  # 超参数
  iters_num = 10000  # 适当设定循环的次数
  train_size = x_train.shape[0]
  batch_size = 100
  learning_rate = 0.1
  
  train_loss_list = []
  train_acc_list = []
  test_acc_list = []


​  
​  for i in range(iters_num):
​ #  获取mini-batch
​ batch_mask = np.random.choice(train_size, batch_size)
​ x_batch = x_train[batch_mask]
​ t_batch = t_train[batch_mask]
​ 
 # 计算梯度
 # grad = network.numerical_gradient(x_batch, t_batch)
 grad = network.gradient(x_batch, t_batch)
 
 # 更新参数
 for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
 
 loss = network.loss(x_batch, t_batch)
 train_loss_list.append(loss)

mini-batch 的大小为 100，需要每次从 60000 个训练数据中随机取出 100 个数据（图像数据和正确解标签数据）。然后，对这个包含 100 笔数据的 mini-batch 求梯度，使用随机梯度下降法（SGD）更新参数。这里，梯度法的更新次数（循环的次数）为 10000。每更新一次，都对训练数据计算损失函数的值，并把该值添加到数组中。

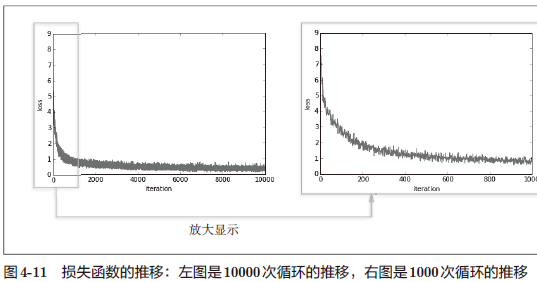
image.png

4.5.3 基于测试数据的评价

上面这个损失函数的值，严格地讲是“对训练数据的某个 mini-batch 的损失函数”的值。训练数据的损失函数值减小，虽说是神经网络的学习正常进行的一个信号，但光看这个结果还不能说明该神经网络在其他数据集上也一定能有同等程度的表现。
神经网络的学习中，必须确认是否能够正确识别训练数据以外的其他数据，即确认是否会发生过拟合。
要评价神经网络的泛化能力，就必须使用不包含在训练数据中的数据。

下面的代码在进行学习的过程中，每经过一个 epoch 会记录下训练数据和测试数据的识别精度。
一个 epoch 表示学习中所有训练数据均被使用过一次时的更新次数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
  import sys, os
  sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
  import numpy as np
  import matplotlib.pyplot as plt
  from dataset.mnist import load_mnist
  from two_layer_net import TwoLayerNet
  
  # 读入数据
  (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
  
  network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)
  
  iters_num = 10000  # 适当设定循环的次数
  train_size = x_train.shape[0]
  batch_size = 100
  learning_rate = 0.1
  
  train_loss_list = []
  train_acc_list = []
  test_acc_list = []
  # 平均每个epoch的重复次数
  iter_per_epoch = max(train_size / batch_size, 1)
  
  for i in range(iters_num):
 batch_mask = np.random.choice(train_size, batch_size)
 x_batch = x_train[batch_mask]
 t_batch = t_train[batch_mask]
 
 # 计算梯度
 #grad = network.numerical_gradient(x_batch, t_batch)
 grad = network.gradient(x_batch, t_batch)
 
 # 更新参数
 for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
 
 loss = network.loss(x_batch, t_batch)
 train_loss_list.append(loss)
 # 计算每个epoch的识别精度
 if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

之所以要计算每一个 epoch 的识别精度，是因为如果在 for 语句的循环中一直计算识别精度，会花费太多时间。没有必要那么频繁地记录识别精度（只要从大方向上大致把握识别精度的推移就可以了）。

image.png

​

深度学习 > 入门
深度学习入门+前四章
http://example.com/posts/30538.html
作者
司马吴空
发布于
2023年8月6日
许可协议